Vibrations
2 Anatomy of a vibration

Any back and forth motion is called a vibration. Examples are everywhere- kids on playground swings, plucked strings, weights attached to springs, and so on. Many objects that wiggle back and forth- like vocal cords, stereo speakers and tuning forks- cause ripples in the air that are detected by our ears as sound.
Frequency
Vibrations that are regular and predictable- like pendulums- are called periodic. Periodic vibrations are at the heart of music, human speech and almost any other sound where humans perceive pitch. Frequency is the measure of how often cycles repeat- the number of cycles in a given amount of time.
Mathematically, frequency is represented by a lower case script [latex]f[/latex]. In mathematical terms:
[latex]f = \frac{number \: of \: cycles \:} {amount \: of \: time \: for \: those \: cycles}[/latex]
For example, when an audio speaker cone goes in and out 8000 times in 2 seconds, the speaker’s frequency is 8000 cycles divided by 2 seconds, or 4000 cycles per second, or 4000 Hz. Hertz (abbreviated Hz) are the same thing as cycles per second. The Hertz is the official metric system unit for frequency, so you can use metric prefixes (like kilo- and mega-) with Hertz. For example, a radio station at 91.3 MHz creates 91.3 million cycles of radio waves every second!
Units matter!
Throughout the book, you will see green boxes like this one highlighting the important role of units in science.
Every scientific quantity (like 5.4 meters) is a number (like 5.4) multiplied by a unit of measure (like meters). Both the unit and the number matter!
Always include the units! What does “5.4” stand for? A weight in grams? A time in centuries? Without units, it’s impossible to tell!
Learn the math of units! Scientific quantities behave slightly different than numbers in math class- 10.8 ounces does not equal 10.8 grams, but 1 hour does equal 60 minutes. The rules for numbers from math class work for scientific quantities, but you must consider both the number and its unit.
Keep the units in your math! Label your quantities with units and follow the units through your math. This will help you make sense of your answer and sometimes help you spot (and avoid) mistakes.
Period
Another way to think about the “speed” of vibrations is in terms of the vibration’s period. Period is the amount of time it takes for one full cycle of a vibration. Mathematically, period is represented by the lower case Greek letter tau ([latex]\tau[/latex]). Here’s the mathematical definition of period:
[latex]\tau = \frac{amount \: of \: time}{number \: of \: cycles \: during \: that \: time}[/latex]
Period and frequency are inverses of each other- when frequency is high, each cycle of the vibration takes very little time. You’ll notice that equations for frequency and period are reciprocals of each other (like the fractions 3/7 and 7/3). As a result,
[latex]f = \dfrac{1} {\tau}[/latex]
or equivalently,
[latex]\tau = \dfrac{1} {f}[/latex]
If you know the frequency, you automatically know the period, and vice versa. A vibration with a frequency of 20 Hz completes 20 full cycles in a second, so each cycle takes 1/20th of a second. The table below shows the frequency and (corresponding) period for some common “vibrations.”
| Frequency (in Hz) |
Period (in sec) |
|
| Human heartbeat | ~1 | ~1 |
| Lowest note on the piano | ~30 | ~0.03 |
| Highest note on the piano | ~4,000 | ~0.0002 |
| CD sampling rate | ~40,000 | ~0.00002 |
| Cell phone processor | 2,000,000,000 | ~0.0000000005 |
Vibrations with periods longer than 1 sec (or frequencies less than 1 Hz) are sometimes called oscillations.
Stop to think 1
A bee flaps its wings about 200 times per second, while an eagle flaps its wings about 5 times per second. Which motion has the longer period? Which has the greater frequency? (Scroll to the end of this chapter to check your answers).
Example: Hummingbird wingbeats
Some hummingbirds can flap their wings 5000 times per minute when they hover. What is the frequency of hummingbird wingbeats (expressed in Hertz)? How long does a single wingbeat take?
To find the frequency of wingbeats, you need to use the definition of frequency. To get the result in Hertz (i.e. cycles per second, make sure to plug the time in seconds into the equation. There are 500 cycles every minute, so
[latex]f = \frac{number \: of \: cycles \:} {amount \: of \: time \: for \: those \: cycles}=\frac{5000 \: \text{cycles}} {60 \: \text{s}}=83 \: \text{Hz}[/latex]
If you’ve seen a hummingbird hover, you know it delivers a low pitched hum, so the answer of 83 Hz seems reasonable- it’s near the low end of human hearing (as you will read in the next section).
To find the period, use the defining equation for period. Again, use the time in seconds to make sure your answer is expressed in seconds:
[latex]\tau = \frac{amount \: of \: time}{number \: of \: cycles \: during \: that \: time}=\frac{60\: \text{s}} {5000 \: \text{cycle} }= 0.012 \: \text{s/cycle}[/latex]
This is means each wingbeat takes a little more than one-hundredth of a second.
About units: When you “plug numbers into a science equation,” always bring the units “along for the ride.” Suppose I had plugged in “1” for time when I was finding period. I’d get an answer of 0.0002. Without units, it’s not clear what the number means. However, if I plug in “1 minute” for time, the meaning of the answer is clear- it’s 0.0002 minutes/cycle (which is the same thing as 0.012 seconds/cycle).
Dealing with units: What does 1/Hz mean?
Suppose you want to find the period of a 5000 Hz vibration. If you use the equation [latex]\tau = \dfrac{1} {f}[/latex] and plug in values you get
[latex]\tau = \dfrac{1}{f}=\dfrac{1}{5000 \: \text{Hz}}=0.0002 \dfrac{1}{\text{Hz}}=??[/latex]
But what does 1/Hz mean? Since Hz stands for cycles per second, 1/Hz must be the reciprocal of that- seconds per cycle. So…
[latex]\tau=0.0002 \dfrac{1}{\text{Hz}}=0.0002 \dfrac{\text{s}}{\text{cycle}}[/latex]
So the period is 0.0002 seconds. (Physicists and others often drop the “per cycle” when talking about period).
The takeaway is this: any time you see 1/Hz, you can replace it with sec/cycle or with seconds- either is OK.
Frequency and sound
Human sensation of pitch is built on frequency. We hear low frequency vibrations as low pitched- think tuba or foghorn. High frequency vibrations are perceived as high pitched sounds- think piccolo. Most people can hear sounds with frequencies as low as about 20 Hz to as high as about 20,000 Hz (20 kHz). If you’re a musician, you probably know that musical note names are based on frequencies. Musical scales and intervals are based on frequency ratios. More details on this can be found later in this book.
If you’re not a musician, take a minute to play with a virtual piano (like the one at https://www.musicca.com/piano) to make sure you know what pitch is. The keys are arranged by frequency/pitch, with the lowest notes at the left end of the keyboard.
Most sounds have frequencies that change. The changes can be slow, like a melody, or fast, like the inflections in human speech or bird calls. These are called quasi-periodic vibrations. If frequency is steady for even a short amount of time- a few milliseconds is enough- the sound is perceived as musical or pitched. Even sounds that don’t seem especially musical, like human speech, often involve quasi-periodic vibration.
Some sounds are caused by vibrations that don’t repeat at all. These are called aperiodic vibrations. Transients and noise are examples of aperiodic vibrations. Transients don’t last very long- things like a popping balloon or the crack of a whip. Noise refers to random vibrations that last a little while- the object moves back and forth for a long time, but there is no pattern to the motion. Random vibrations cause sounds like static on the radio or air rushing out of a tire or the librarian’s “shhhh.”
Amplitude
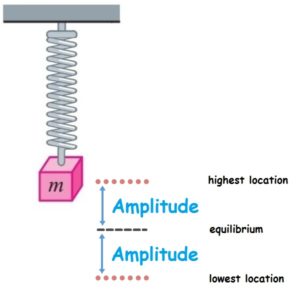
Amplitude describes “how large” a vibration is. Amplitude can be measured in almost any units, depending on what’s fluctuating.
Amplitudes based on location (often called displacement amplitudes) are the easiest to visualize. Imagine a weight that bobs up and down between two locations 6 cm apart. The displacement amplitude is 3 cm. (Amplitude is measured from the middle to one extreme- not from one extreme to the other).
Amplitudes don’t have to be based on location. In sound, air pressure fluctuates so pressure amplitude is most basic way for describing sound amplitude. Pressure amplitude is measured in Pascals (Pa), the international unit for pressure. In the recording studio, electrical signals (measured in Volts) fluctuate, so amplitudes are measured in Volts. For example, if an electrical signal varies between 2.3 V and 3.3 V, the amplitude is 0.5 V.
Stop to think 2
While you listen to the stereo, air pressure in your ear might vary between 101,200.5 Pa and 101,200.7 Pa. What is the pressure amplitude of this sound? (The abbreviation “Pa” stands for “Pascal”- the metric unit for pressure).
Amplitude and sound
The human sensation of loudness depends mainly on pressure amplitude (though frequency also plays a role). In general, the larger the pressure amplitude a sound has, the louder it sounds. Human ears are incredibly sensitive. We easily detect sounds that have pressure amplitudes as small as 20 microPascals- which is less than one billionth of atmospheric pressure (which is about 100,000 Pa).
Though technically not an amplitude, decibels (abbreviated dB) are a common way to express the size of pressure variations in a sound. Decibels uses logarithms to transform pressure amplitude numbers into a much more human-friendly format. Most everyday sounds fall between 0 dB (for things we can just barely hear) to 100 dB (for super loud power tools). The table below compares pressure amplitudes (in microPascals) and sound pressure levels (in dB) for some everyday sounds.
| Sound | Pressure amplitude (in μPa) |
Sound Pressure Level (in dB) |
| Hearing threshold | 20 | 0 |
| Rice krispies | 600 | 30 |
| Conversation | 20,000 | 60 |
| Leaf blower | 600,000 | 90 |
| Loud indoor arena | 20,000,000 | 120 |
More details about the relationship among loudness, pressure amplitude, and decibels can be found later in the book.
Online resources
At the end of most sections of this book, you will find links to online content pertaining directly to the material you’ve just read. For best results, try to view/explore as many of these resources right after doing the reading. (A fuller list of resources can be found in the “Electronic resources” in the Useful Information section of this book).
View Measuring Frequency (a 2:26 youTube video) [1]. This video leads you through how to measure period (and frequency) for a spring-mass oscillator, including the numerical calculations.
Play with the animation SpringMassPend (a Desmos simulation)[2]. Play with the sliders for frequency and amplitude and see how the motion changes. BTW, this simulation was written using the free online graphing calculator at Desmos.com, developed by Texas Instruments. If you like math even a little bit, learn Desmos yourself. It’s easy and fun!
Stop to Think Answers
Stop to think answers
- The eagle’s flapping has the longer period. The bee’s wings flap more frequently.
- The pressure amplitude of the sound is 0.1 Pa. (Subtract the lowest pressure from the highest and divide by two). Notice that the variation in air pressure in the sound is extremely small compared to the average air pressure.
Image credits
- Accutron Watch: https://commons.wikimedia.org/wiki/File:Accutron.jpg
- Amplitude diagram: created by David Abbott
