Interference
35 How to make standing waves
Making standing waves
Traveling waves are formed when a vibrating source is placed in a material. How are standing waves formed? Standing waves have nodes- locations where there’s no motion at all. Could this be an example of destructive interference?
Two identical waves traveling in opposite directions
What happens if you point two identical wave sources at each other? It’s pretty clear that two waves will interfere, but how will the two waves combine? Try it in the real world and you discover that the result is a standing wave. Simply point two loudspeakers at each other and play the same pure tone through both speakers and you will discover nodes- “dead spots” where there is no sound at all- spaced at regularly spaced distances. Researchers have used standing waves created by two speakers to suspend really light objects (water droplets and small styrofoam balls) in midair. This acoustic levitation is demonstrated in a 1:03 youTube video by Argonne National Laboratory. [1] An acoustic levitation video by Harvard’s science demo group (4:33) [2] creates the standing wave by reflecting a sound back on itself and uses Schlieren photography to show the nodes and antinodes.
The standing wave that is created by two identical waves traveling in opposite directions has the same wavelength and frequency as the two traveling waves that were used to create it. For example, a single speaker that plays a 340 Hz tone produces a traveling wave with a wavelength roughly 1.0 meter long. When two speakers playing a 340 Hz tone face each other, they produce a standing wave with a wavelength of 1.0 meter between the two speakers. Keep in mind that this does not mean that the nodes are 1.0 meter apart- the nodes are only 0.5 meters apart. Remember that the wavelength of a standing wave is twice the node spacing.
Stop to think
- Two audio speakers pointed at each other both emit the same equally loud pure tone. The sound has a wavelength of 2.0 meters. Will there be locations where there is no sound? Where? How far apart?
How traveling waves combine to make the standing wave
How do two identical traveling waves traveling in opposite directions form a standing wave? The principle of superposition explains how it’s possible. A complete proof is easy, but tedious. Simply apply the principle of superposition to two identical traveling waves going in opposite directions and look at the results. Animation of the result can be seen on the Physics Classroom’s Formation of Standing Waves web page [3] or on the Superposition page [4] of Dan Russell’s website.
What makes a standing wave unique is the presence of nodes- locations in the medium that never move. Show that two identical waves traveling in opposite directions create a standing wave, and you’ve gone a long way toward proving that a standing wave is being formed. The figure below shows how it happens.
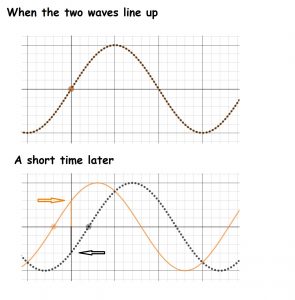
Start by examining a moment when the two waves are perfectly aligned. At this moment, there are many locations that have zero displacement- simply because the zeros on both waves line up. These spots are probably where the nodes are formed. If these spots are really nodes, the total displacement at these locations will always be zero. To check, let’s look at the waves a short time later. As one wave moves to the right, the other moves to the left by the same amount (because both waves are traveling at the same speed). Where both waves used to have zero displacement, one wave now has a positive displacement and the other has negative displacement. However, the total displacement is still zero. Because of the way sine waves are shaped, the negative displacement from one wave exactly cancels out the positive displacement from the other. It doesn’t matter how much time passes, either- the total displacement at this location will always be zero– positive displacement from one wave will always align with an exactly equal negative displacement from the other because of the way sine waves are shaped. As the identical traveling waves pass through each other, they interfere to create nodes. You can explore the ideas in this paragraph by playing with the Desmos simulation StandingWaveFormation2. [5]
Stop to think
- Is it possible to form standing waves from two waves traveling in the same direction? Explain.
- Is it possible to form standing waves from two traveling waves with different amplitudes? What happens when the amplitudes are different?
Stop to think answers
- There will be dead spots (nodes) in between the two speakers. The nodes will be spaced 1.0 meters apart.
- No. When both waves move in the same direction, are always shifted (relative to each other) by the same amount. The superposed wave, as a result, is a traveling wave.
- No. There won’t be any nodes. There will be times when the waves are perfectly aligned and there will be locations with zero displacement. However, a short time later, the displacement at these locations will no longer be zero- the positive displacement of one wave does not equal the negative displacement of the other (because the amplitudes don’t match).
Image credits
- Using sound waves to suspend droplets. Photo by Dan Harris/Argonne National Lab, obtained from WikiMedia Commons) [6]
- Identical waves traveling in opposite directions for a standing wave. Created by Abbott using desmos.com.
- Argonne National Laboratory. (2012, September 12). Acoustic levitation. Retrieved from https://youtu.be/669AcEBpdsY ↵
- Harvard Natural Sciences Lecture Demonstrations. (2017, February 23). Ultrasonic levitation. Retrieved from https://youtu.be/XpNbyfxxkWE ↵
- The Physics Classroom. (no date). Standing Wave Formation. Retrieved from https://www.physicsclassroom.com/mmedia/waves/swf.cfm ↵
- Russell, D. (2014, January 27). Superposition. Retrieved from https://www.acs.psu.edu/drussell/Demos/superposition/superposition.html ↵
- Abbott, D. (2018, July 19). MakeStandingWave2. Retrieved from https://www.desmos.com/calculator/fzv3ni7eit ↵
- Harris, D. (2012, October 19). Acoustic levitation. Retrieved from https://commons.wikimedia.org/wiki/File:October_19,_2012-_Acoustic_Levitation_for_Medicine_(8125198677).jpg ↵
