Musical instruments
28 Vibrating air columns
Wind instruments
Wind instruments, like the flute and the trombone are made of tubes or pipes. How do these instruments work? What material is vibrating? What is the function of the pipe? How does the length of a pipe affect the pitch of the sound it produces?
A quick look at the orchestra reveals that instruments with longer pipes generally produce lower notes- compare the trumpet and the tuba, for instance. What’s actually happening?
Vibrating air columns
The air inside the pipes of a wind instrument vibrates. The tubing in a wind instrument confines the motion of the air inside it- the air particles must wiggle parallel to the walls of the pipe. The result is a longitudinal standing wave in the air column inside the pipe. The ends, whether open or closed, create nodes or antinodes.
On a string, the reason for nodes at the ends of standing wave on a string is obvious. Something (a person, the nut of a string instrument, etc.) holds the string and prevents it from vibrating. The cap on the closed end of a pipe does essentially the same thing by preventing air from leaving (or entering) the pipe. Air particles at the closed end don’t move at all, creating a displacement node. At displacement nodes, the density and the pressure of the air fluctuates wildly molecules crowd together and spread apart. As a result, displacement nodes are sometimes called pressure antinodes. The open end of a tube also acts a sort of clamp. Near the open end of a pipe, air molecules can enter or leave the tube easily. However, the pressure near the end of the tube must match the pressure in the room (which doesn’t fluctuate at all). As a result, particles near the end of the tube oscillate back and forth with large amplitude. The result is a displacement antinode. At displacement antinodes, the density of particles remains constant as the particles slosh back and forth across the equilibrium position. So, displacement antinodes are also pressure nodes. To see how this works, the reader is strongly encouraged to visit Dan Russell’s web page on standing waves in air columns [1] while rereading this paragraph, focusing on the animations that show the motion of air particles.
Different representations
Longitudinal waves are hard to draw, so many books show diagrams for air column standing waves that look like transverse waves. Instead of showing how the air particles are moving, these diagrams show graphs of displacement versus position along the direction of the column. Here’s what the diagrams usually look like:
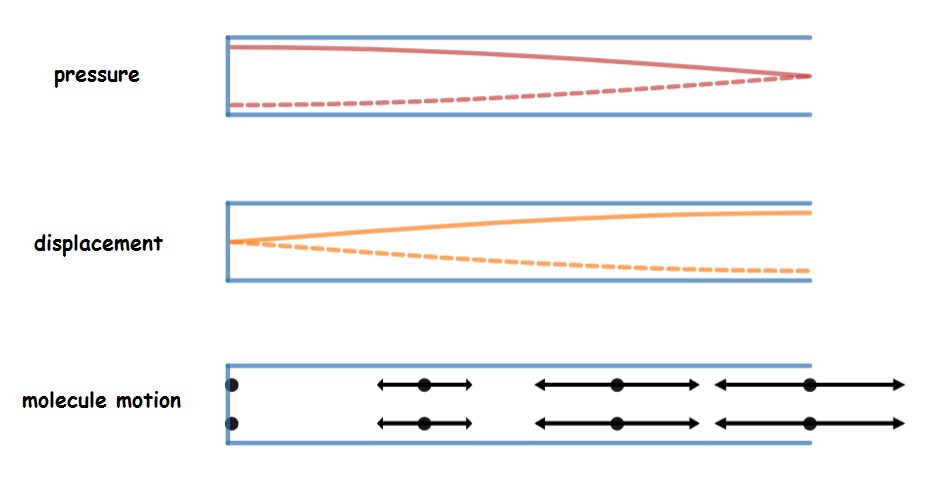
The diagram summarizes the connections among particle motion, displacement and pressure for standing waves in air columns. All three diagrams show the fundamental mode of a pipe closed at one end. The bottom picture shows how the molecules move at different locations in the tube. Particles don’t move near the closed end of the tube, while particles near the open end vibrate back and forth. The next diagram up is called a displacement graph. This diagram also shows how much particles move at various locations within the tube, but in a different way- where the particles don’t move, the displacement is zero and the graphs shows zero (like at the closed end of the tube). Large displacement amplitude is shown where the graph is away from the center line (like at the open end of the tube). The top diagram is somewhat different. The top graph shows how much pressure oscillates at various locations in the tube- large pressure variations happen where the graph is far off the center line (like at the open end of the tube).
Pressure vs. displacement
Notice that the pressure graphs and displacement graphs are “opposites” of each other- pressure nodes are displacement antinodes (and vice versa). This is because particles move most where the pressure is steady and pressure fluctuates wildly where particles are not allowed to move freely.
Both types of graphs are useful. The displacement graphs indicate where particles move most and least. Pressure graphs indicate where the sound will be loudest- keep in mind that loudness perception is based on how much the pressure changes in the wave- the larger the pressure fluctuations, the louder the sound.
Open-open
Pipes that are open at both ends have pressure nodes at both ends, so the pressure versus position graphs (shown below) look a lot like standing wave patterns on a string. Standing waves are formed when a whole number of “footballs” fit in the length of the tube.
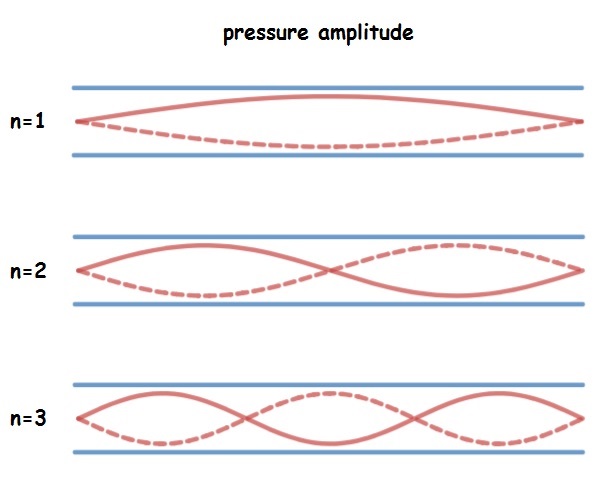
As a result, the equations for open-open air columns look identical to equations for strings:
[latex]\lambda_n=\frac{2L}{n}[/latex]
[latex]f_n=nf_1[/latex]
[latex]f_1=\frac{v}{2L}[/latex]
Now, [latex]L[/latex] represents the length of the tube (rather than string length) and [latex]v[/latex] is the speed of sound in air- not the speed of waves in a string.
As with the string, the frequencies of all modes are whole number multiples of the fundamental- an open/open tube with a fundamental of 100 Hz produces overtones of 200 Hz, 300 Hz, 400 Hz, etc.
Stop to think 1
A whirly tube is a corrugated pipe, open at both ends. The toy makes a pitched sound when you whirl it over your head like a lasso.

- What is the fundamental wavelength of a whirly tube that is 80 cm long?
- When you twirl a whirly tube, you find that the lowest pitch it can produce is 600 Hz. As you spin it faster, the next note it produces is 800 Hz. Is the 600 Hz note the fundamental frequency of the tube? If not, what is the fundamental frequency?
Open-closed
For tubes open at one end and closed at the other, there is a pressure antinode at the closed end of the tube and a pressure node at the open end. As a result, standing waves are only formed when an odd number of “half-footballs” fits in the length of the tube.
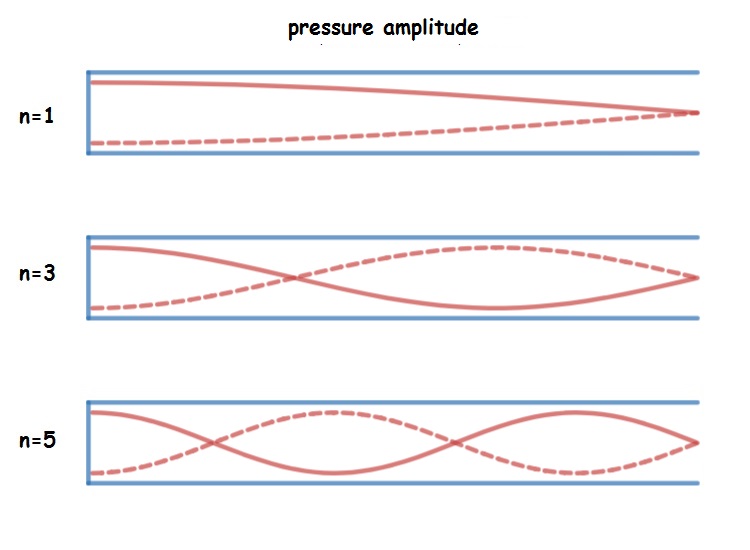
Not surprisingly, the equations for open-closed air columns are slightly different than for open-open. The most striking difference is that only odd numbers are allowed for [latex]n[/latex]. This is because there is node at one end of the tube, but an antinode at the other. The other difference is that [latex]2L[/latex] for open-open is replaced by [latex]4L[/latex].
[latex]\lambda_n=\frac{4L}{n}[/latex]
[latex]f_n=nf_1[/latex]
[latex]f_1=\frac{v}{4L}[/latex]
[latex]n[/latex] must be odd
The equations have two important implications. First, open-closed tubes only produce overtones at odd multiples of the fundamental: an open-closed tube with a fundamental of 100 Hz produces overtones of 300 Hz, 500 Hz, 700 Hz and so on. This gives open/closed tubes a different timbre than open/open tubes. Second, an open-closed tube has a lower fundamental than an open-open pipe of the same length by a factor of two in frequency (a.k.a. one octave lower).
Stop to think 2
A BoomWhacker is a plastic tube that makes pitched sound when you whack it. The toy comes with a plastic cap that can cover one end of the tube. What is the fundamental wavelength of a BoomWhacker that is 70 cm long if the cap is off? What is the fundamental wavelength of the same tube with the cap on?
End corrections
The simplistic model above assumes that the radius of the pipe doesn’t matter. However, experiments with pipes show that radius matters- fatter pipes have slightly lower pitches than skinnier ones of the same length. The reason is that the pressure nodes at the open ends of real air columns are located slightly outside the end of the tube- how far outside depends on the radius of the pipe. To good approximation, the distance from the physical end of the tube to pressure node is 0.3 times the diameter of the tube. This distance is called the end correction. Fatter pipes need larger end correction.
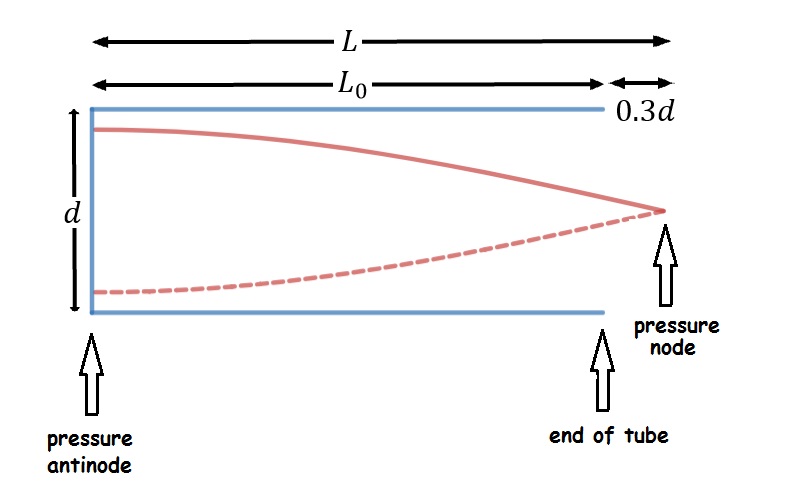
There is no end correction for the closed end of a pipe- the pressure antinode is right at the end of the pipe, so the effective length of an open-closed air column is slightly longer than the pipe itself:
[latex]L=L_0+0.3d[/latex]
In this equation, [latex]L[/latex] represents the effective length of the air column, [latex]L_0[/latex] represents the physical length of the pipe and [latex]d[/latex] represents the diameter of the pipe.
For an open-open air column, the standing wave extends beyond the tube at both ends, as shown below.
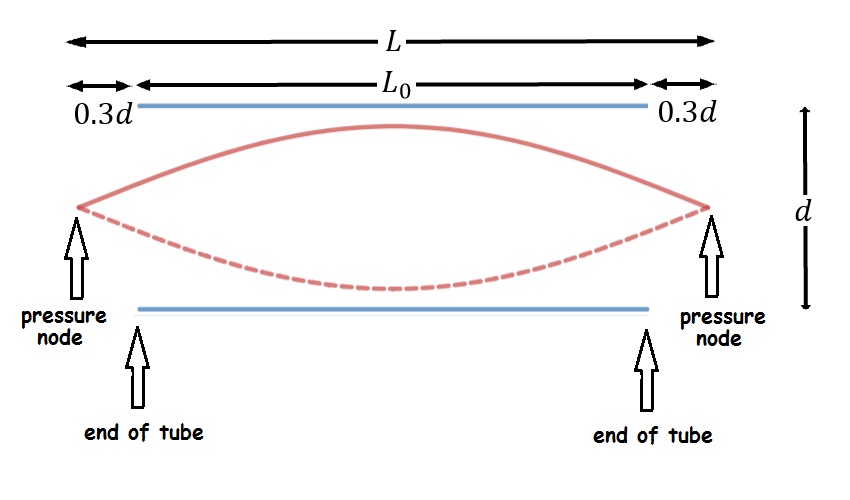
As a result, the effective length for open-open air columns is
[latex]L=L_0+0.6d[/latex]
To apply the end correction, calculate the effective length of the air column and use that value in all of the air column equations (instead of using the length of the tube).
Stop to think answers
- The fundamental wavelength is twice the length of the tube (or 160 cm). For open-open air columns, resonant frequencies are whole number multiples of the fundamental. If the tube produces 600 Hz and 800 Hz (and no notes in between), the fundamental must be 200 Hz. (For why the whirly won’t sing in the n=1 and n=2 modes, read this journal article on singing corrugated pipes).
- With the cap on, the n=1 wavelength is twice the length of the tube (or 140 cm). With the cap on, the n=1 wavelength is four times the length of the tube (or 280 cm).
Image credits
Three equivalent representations of the n=1 mode in an air column closed at one end. Created by Abbott using desmos.com.
Pressure amplitude in an air column open at both ends. Created by Abbott using desmos.com.
Whirly tube (a.k.a. corrugaphone). Chridd via Wikimedia Commons [2]
End correction for open-closed air column. Created by Abbott using desmos.com.
End correction for an air column open at both ends. Created by Abbott using desmos.com.
